Министерство образования и науки РФ
МГУ им. М.В.Ломоносова
Мехмат МГУ
Кафедра высшей геометрии и топологии
|
|
Основные направления исследованийБесконечномерные интегрируемые системы математической физики
|

|
(Мануйлов, Троицкий, Мищенко, Миллионщиков, Пенской и др.)
В основе применения методов некоммутативной геометрии в математической физике лежит аналогия между квантованием и основной идеей перехода от коммутативной к некоммутативной геометрии, заключающейся в следующем. Рассмотрим "хорошее" топологическое пространство X. Ему можно поставить в соответствие C*-алгебру... Читать далее »Комбинаторная топология, многогранники
(Бухштабер, Панов, Гайфуллин и др.)
Общая теория действий тора имеет длинную историю развития и образует важную область эквивариантной топологии. По мере того, как область её приложений разрасталась, возникла целая новая область под названием торическая топология. Торическая топология изучает алгебраические, комбинаторные, дифференциальные и гомотопические аспекты класса действий тора, для которых пространство орбит несёт богатую комбинаторную структуру. Особенностью этой области является... Читать далее »Компьютерные и вычислительные методы
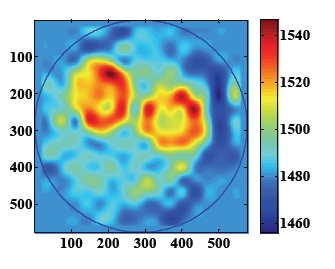
(Клейн, Гриневич, Разумовский и др.)
В лаборатории развивается несколько достаточно независимых друг от друга направлений исследований вычислительного характера. Эти направления условно можно разбить на три группы, каждая из которых тесно связана с фундаментальными теоретическими задачами исследовательских групп. Читать далее »
Телефон: (495) 939-28-84, адрес: Москва, Ленинские горы, 2-й гуманитарный корпус, ауд. 456,
e-mail: dubrovinlab@gmail.com




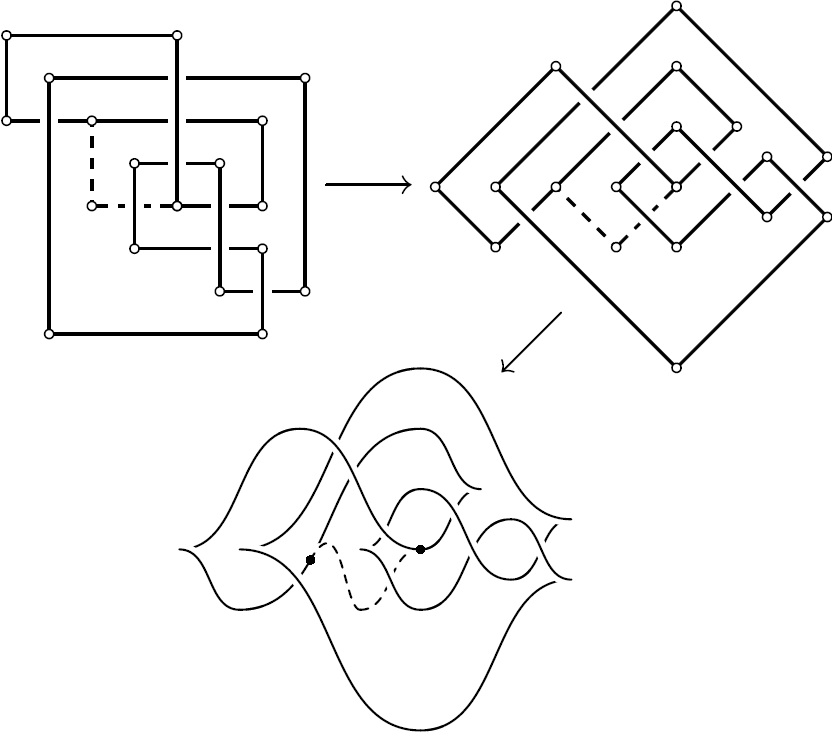 Маломерная топология
Маломерная топология