Лаборатория геометрических методов
математической физики
имени Н. Н. Боголюбова

Компьютерные и вычислительные методы

В лаборатории развивается несколько достаточно независимых друг от друга направлений исследований вычислительного характера. Эти направления условно можно разбить на три группы, каждая из которых тесно связана с фундаментальными теоретическими задачами исследовательских групп.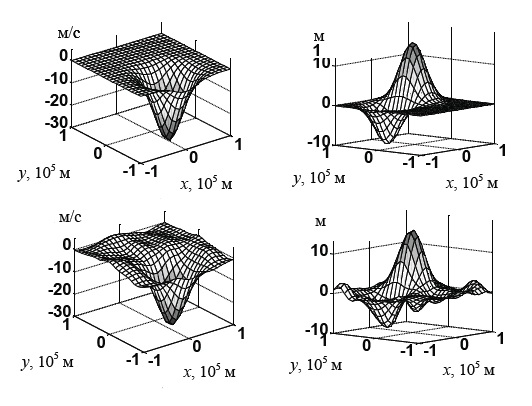

Первое направление вычислений, использующее 3D-процессоры Nvidia (Tesla), связано с практической реализацией метода обратной задачи, развитого П.Г.Гриневичем и Р.Г.Новиковым, в акустической физике, в частности, в акустической томографии океана, которая позволяет восстановить внутреннюю структуру обширных (порядка сотен и тысяч километров) регионов океана на основе характеристик акустических сигналов, прошедших через рассматриваемую область. С математической точки зрения задача акустической томографии океана может быть рассмотрена как частный случай многоканальных обратных задач рассеяния [Novikov R.G., Santacesaria M. Monochromatic reconstruction algorithms for two-dimensional multi-channel inverse problems. – E-print arXiv:1105.4086.], где многоканальность определяется неадиабатичностью распространения акустических мод в океаническом волноводе. Важным шагом в этом направлении стал учет неадиабатического распространения звука, который реализуется функционально-аналитическими методами решения многоканальных обратных задач рассеяния.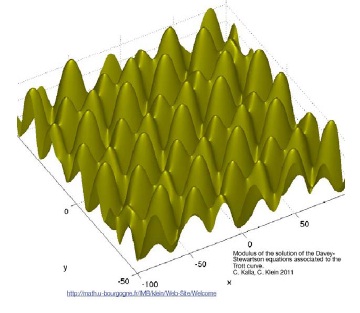

Второе направление вычислительных исследований - численное моделирование уравнений математической физики. В частности, таких известных уравнений как WDVV, уравнение Уизема, двумерное уравнение Шредингера. Изучается поведение решений при изменении параметров, начальных данных и т.п. Одним из последних результатов стала программа для вычисления и визуализации модулированных тэта–функций.

Третье направление - исследование комбинаторных свойств топологических объектов: узлов, зацеплений и более общих объектов, связанных с трехмерными многообразиями. Условно это направление можно назвать "вычислительной топологией". В первую очередь тут следует указать теорию алгоритмической распознаваемости узлов: эти задачи достаточно подробно описаны в разделе "Комбинаторная топология, многогранники". В современной математике "алгоритмическими, вычислительными" часто называют чисто теоретические (возможно очень глубокие) формулировки, не имеющие никакого отношения к реальным вычислениям. Мы хотим подчеркнуть, что реализуемые в рамках лаборатории исследования на самом деле являются "алгоритмическими" в наиболее приземленном понимании этих слов, т.е. с доведением задач до программных продуктов, которые работают на компьютерах. Разработанные И.Дынниковым комбинаторные методы распознавания узлов являются хорошей иллюстрацией наших слов.

Еще один класс задач из "вычислительной топологии" - это изучение плоских сечений 3-периодических поверхностей (Ферми-поверхности). Эти задачи возникли в работах С.П.Новикова при изучении поведения электронов в кристаллических решетках в однородном магнитном поле. Вычислительные эксперименты для "кусочно-плоских" поверхностей с большой интенсивностью проходят на вычислительном комплексе лаборатории. В этой работе дистанционно принимает участие известный специалист из университета Мэриленда Роберто ДеЛео.

Применяемые во всех этих вычислениях методы основываются как на стандартных пакетах (mathematica, matlab, maple), так и на оригинальных программах, разработанных сотрудниками лаборатории. Одним из ключевых методов является использование параллельных вычислений, основанных на аппаратной базе нашей лаборатории (16 двухядерных процессоров). Большое внимание уделяется визуализационной части решений уравнений математической физики: Поскольку стандартные пакеты не справляются со сложностью (2+1) задач, сотрудниками была разработана специальная программа, которая без задержек показывает движение фронта решения некоторых классов уравнений.