Маломерная топология и квантовая теория поля

В рамках данного направления изучаются комбинаторные свойства прямоугольных диаграмм зацеплений, группы кос и классов отображений, периодические поверхности в трехмерном пространстве и R-деревья.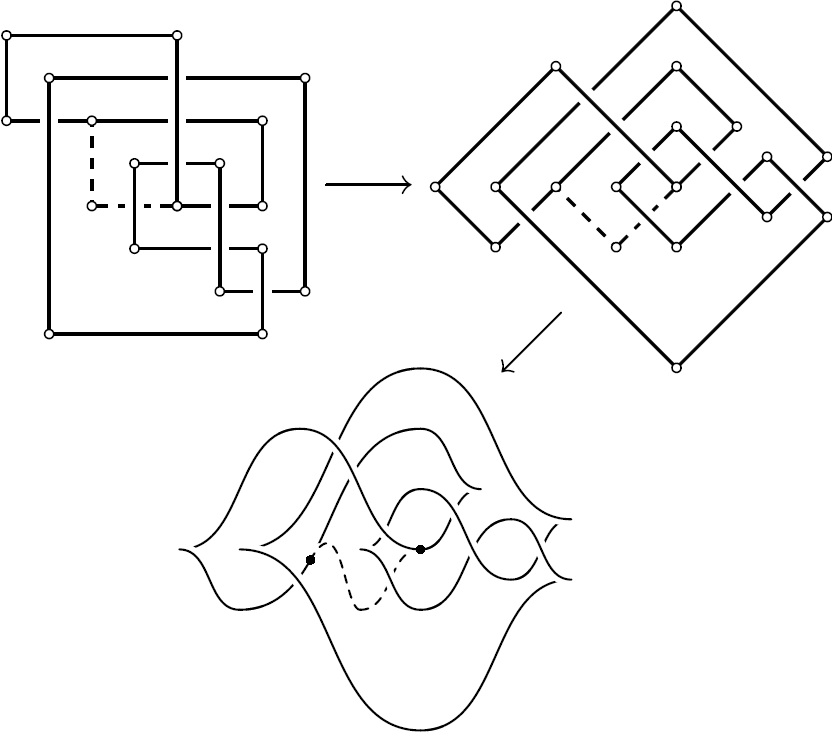

В 2004 г. И.Дынников доказал [1], что все прямоугольные диаграммы тривиального узла допускают монотонное упрощение до тривиальной диаграммы, что дает новый алгоритм для распознавания тривиального узла. Интерес к прямоугольным диаграммам связан также с их независимым появлением в теории гомологий Хегора-Флоера [2], а также тем, что они дают универсальный язык для работы с лежандровыми и трансверсальными узлами [3]. Последнее обстоятельство использовано И.Дынниковым и М.Прасоловым для доказательства, в частности, одной известной гипотезы В.Джонса о том что алгебраическое число пересечений косы на минимальном числе нитей, представляющей данное ориентированное зацепление, является инвариантом зацепления (работа готовится к печати). А.Казанцевым найдены интересные примеры пар прямоугольных диаграмм, задающих эквивалентные зацепления, которые не переводятся друг в друга флайпами [4].

И.Дынниковым и В.Шастиным исследованы некоторые псевдохарактеры на группах кос. Интерес к псевдохарактерам связан, в частности, с тем, что они в некоторых случаях повзоляют указать препятствие к применению к данной косе некоторых операций типа Маркова. Эта теория была ранее развита А.Малютиным [5], который поставил вопрос о линейной зависимости псевдохарактера сигнатуры от псевдохарактеров типа закрученности. В работе Дынникова и Шастина построены новые псевдохарактеры типа закрученности, указаны некоторые новые соотношения между ними и показано, что псевдохарактер сигнатуры от них независим.

Другое направление исследований групп кос и общих групп классов отображений связано с построением эффективных алгоритмов для них. И.Дынников является автором самого быстрого алгоритма (в смысле доказанной теоретической оценки) для решения задачи равенства в группах кос [6]. Этот подход был далее развит Дынниковым и Б.Вистом [7]. Дальнейшая работа направлена, в частности, на построения быстрого алгоритма для решения проблемы сопряженности.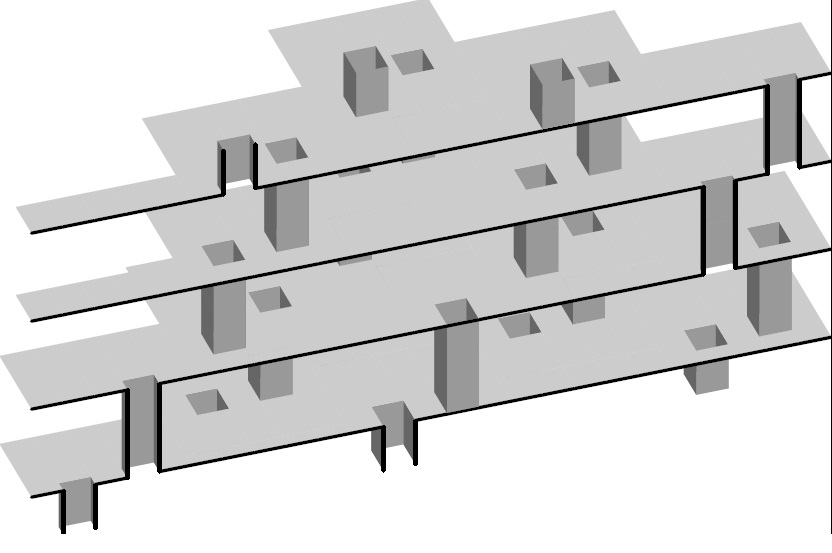

А.Скрипченко продолжает исследования, связанные с плоскими сечениями 3-периодических поверхностей. Изначально задача была поставлена в начале 1980-х С.П.Новиковым в связи с приложением в теории нормальных металлов. В настоящих момент достаточно хорошо изучен так называемый интегрируемый случай задачи [8], [9], и имеется некое описание множества хаотических режимов [10], [11]. Оно основано на так называемых системах наложений отрезков. Для симметричных систем наложений отрезков А.Скрипченко доказала, что индукция Раузи за конечное число шагов снова приводит к симметричной системе [12]. Она исследовала связь конструкции с R-деревьями и показала в некоторых конкретных случаях, что почти все хаотические сечения состоят всего из одной связной компоненты.

Литература

1. I. Dynnikov. Arc-presentations of links: Monotonic simplification, Fund.Math. 190 (2006), 29-761. ( http://arxiv.org/abs/math/0208153)
2. C. Manolescu; P. Ozsvath, Peter; S. Sarkar, A combinatorial description of knot Floer homology. Ann. of Math. (2) 169 (2009), no. 2, 633-660. ( http://arxiv.org/abs/math/0607691)
3. L.Ng, D.Thurston. Grid diagrams, braids, and contact geometry. Proceedings of Gökova Geometry-Topology Conference 2008, 120-136, Gökova Geometry/Topology Conference (GGT), Gökova, 2009
4. A.Kazantsev. The problem of detecting the satellite structure of a link by monotonic simplification. J. Knot Theory Ramifications 20 (2011), no. 1, 109-125
5. А. В. Малютин. Псевдохарактеры групп кос и простота зацеплений. Алгебра и анализ 21:2 (2009), 113-135
6. И. А. Дынников. Об одном отображении ЯнгаБакстера и упорядочении Деорнуа, УМН, 57:3 (345) (2002), 151-152
7. I. Dynnikov; B. Wiest. On the complexity of braids. J. Eur. Math. Soc. 9 (2007), no. 4, 801-840
8. A. V. Zorich, S. P. Novikov's problem of the semiclassical motion of an electron in a homogeneous magnetic field that is close to rational. (Russian) Uspekhi Mat. Nauk 39 (1984), no. 5(239), 235-236.
9. I.A. Dynnikov, Semiclassical motion of the electron. A proof of the Novikov conjecture in general position and counterexamples. Solitons, geometry, and topology: on the crossroad, 45-73, Amer. Math. Soc. Transl. Ser. 2, 179, Amer. Math. Soc., Providence, RI, 1997.
10. I.A. Dynnikov, Interval identification systems and plane sections of 3-periodic surfaces. (Russian) Tr. Mat. Inst. Steklova 263 (2008), Geometriya, Topologiya i Matematicheskaya Fizika. I, 72-84; translation in Proc. Steklov Inst. Math. 263 (2008), no. 1, 65-77
11. R. DeLeo; Ivan A. Dynnikov, Geometry of plane sections of the infinite regular skew polyhedron {4,6 | 4}. Geom. Dedicata 138 (2009), 51-67
12. A. Skripchenko. Symmetric interval identification systems of order three. Discrete Contin. Dyn. Syst. - A 32 (2012), no. 2, 643-656